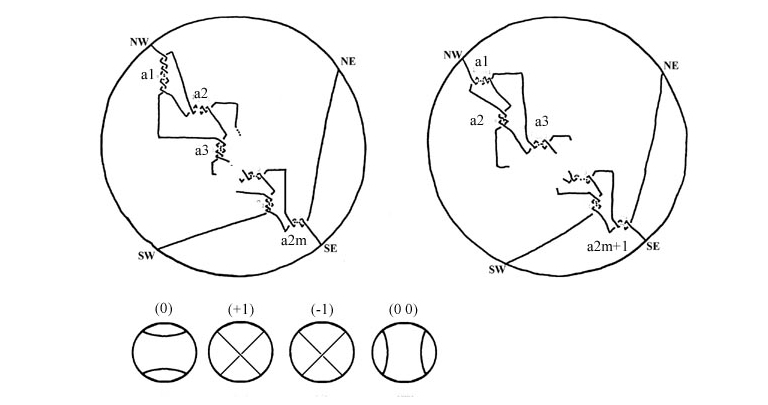
The tangle model is a mathematical method due to De Witt Sumners and Claus Ernst [Sumners et al. Quart. Rev. Biophysics 28, 3 (1995), 253 – 313], which uses knot theory and low-dimensional topology to understand the mechanisms of binding and strand-exchange by site-specific recombinases. A web description of the tangle model can be found here.
DNA unlinking pathways
Work funded by NSF CAREER Award DMS1519375
Multiple cellular processes such as replication, recombination, and packing change the topology of DNA. Controlling these changes is key to ensuring stability inside the cell. The cell uses enzymes to simplify DNA topology. Techniques from knot theory and low-dimensional topology, aided by computational tools, now make it possible for us to study the specific action of such enzymes in these processes. Of special interest is the study of unlinking of DNA replication links by site-specific recombination. We model site-specific recombination as a local reconnection event and study the resulting reconnection pathways. This work is also relevant in fluid dynamics.
The Geometry and Topology of Chromatin During Interphase
Linking between Partially Overlapping Polygons.
NIH funded research (RO1-GM109457)
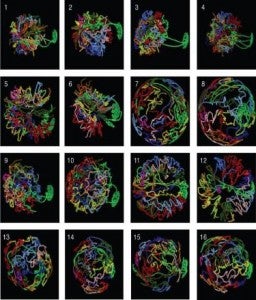
During interphase chromosomes are confined to sub-nuclear regions called chromosome territories. The position of these territories has been associated with a number of biological processes such as cell differentiation and are believed to have a very important role in cancer and other human diseases.
We are developing statistical methods that interrogate mFISH or SKY data for chromosome clustering (i.e. for deviations from randomness in the relative positions of chromosomes). Our approach is based on the hypothesis that chromosomes that are in close proximity form radiation induced chromosome aberrations more often than those that are far apart (known as the proximity effect hypothesis). When applying these methods to human lymphocytes we find two sets of chromosomes that are on average closer to each other than what randomness would predict these are: {1,16,17,19,22}and {13,14,15,21,22} (Cornforth et al. 2002, Arsuaga et al. 2004, Vives et al. 2005). We have recently investigated the topology of the interface between chromosome territories assuming that the chromatin follows the trajectory of a random walk. We have found that the probability that two territories are topologically linked grows as 1-O(1/sqrt(nm)) where n and m correspond to the length of the polygons.
Videos:
Packing, Folding and Simplifying DNA Topology, lecture presented at the Molecular Biosciences Institute during the workshop Geometric and Topological Modeling of Biomolecules
DNA packing in bacteriophage capsids
NSF funded research DMS 0920887 (2009-2014)
DNA presents high levels of condensation in all organisms. We are interested in the problem of DNA packing inside bacteriophage capsids. Bacteriophages are viruses that infect bacteria, and DNA extracted from bacteriophage P4 capsids is highly knotted. These knots can shed information on the packing reaction and DNA architecture inside the capsid.
Videos:
DNA packing research was featured in Numberphile:
Minicircle Organization in kDNA Networks of Trypanosomes
NSF funded research DMS 0920887 (2009-2014) — Selected for NSF Highlights 2011
Trypanosomes are protozoa which cause fatal diseases such as sleeping sickness and Chagas disease. These diseases are catalogued as neglected by the World Health Organization. A distinctive feature of trypanosomatid parasites is that their mitochondrial DNA, known as kinetoplast DNA, is organized into thousands of minicircles and a few dozen maxicircles. Furthermore, minicircles in these organisms are topologically linked, forming a gigantic network in which the minicircles are interlocked in a chain mail-like structure). We study the topological structure of the minicircles.